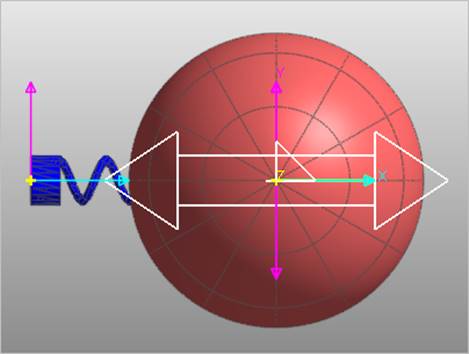

Figure 1 Example model
•DOF is 1 and EOM is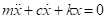 .
.
•Sphere, translational joint and spring force
•No gravity ( or Simulates both static analysis and Eigenvalue analysis)
•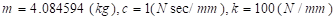
•Result
|
Expression |
Result |
|
Undamped natural frequency (Hz) |
2.490266E+01 |
|
Real of damped Eigenvalue (/2PI) |
-1.948235E+01 |
|
Imaginary of damped Eigenvalue (Hz) (Damped frequency) |
+/- 1.551066E+01 |
|
Damping ratio |
7.823400E-01 |
Critical damped case
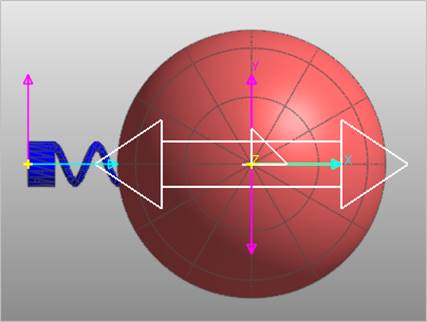
Figure 2 Example model
•DOF is 1and EOM is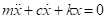 .
.
•Sphere, translational joint and spring force
•No gravity ( or Simulates both static analysis and Eigenvalue analysis)
•Can compute the critical damping from Example A.
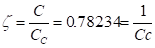 (20)
(20)
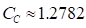 (21)
(21)
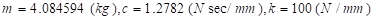
•Result
|
Expression |
Result |
|
Undamped natural frequency (Hz) |
2.490266E+01 |
|
Real of damped Eigenvalue (/2PI) |
-2.490233E+01 |
|
Imaginary of damped Eigenvalue (Hz) (Damped frequency) |
+/- 1.268287E-01 |
|
Damping ratio |
9.999870E-01 |
•Damping ratio is approximated 1.0.
Over damped case

Figure 3 Example model
•DOF is 1 and EOM is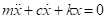 .
.
•Sphere, translational joint and spring force
•No gravity (or Simulates both static analysis and Eigenvalue analysis)
•In over damped case damping coefficient is greater than critical damping coefficient.
•
•Result
|
Mode |
Expression |
Result |
|
1 |
Undamped natural frequency (Hz) |
0.000000E+00 |
|
Real of damped Eigenvalue (/2PI) |
-6.893309E+01 | |
|
Imaginary of damped Eigenvalue (Hz) (Damped frequency) |
0.000000E+00 | |
|
Damping ratio |
1.000000E+00 | |
|
2 |
Undamped natural frequency (Hz) |
0.000000E+00 |
|
Real of damped Eigenvalue (/2PI) |
-8.996294E+00 | |
|
Imaginary of damped Eigenvalue (Hz) (Damped frequency) |
0.000000E+00 | |
|
Damping ratio |
1.000000E+00 |
•In over damped case, damped frequency is all zero (0.0 Hz). Because, damped Eigenvalue has only two real values in the same mode shape.
•And reported undamped natural frequency and damping ratio have no meaning. Because, undamped natural frequency is analytically computed using critical and underdamped case definition. So, when number of reported modes are greater than DOF of system, check the over damped system exists using under damped type.