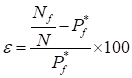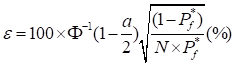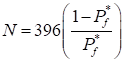Accuracy and Efficiency of Estimation
The accuracy of the estimate of  may depend on the number of sample
points(
may depend on the number of sample
points(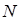 ). A small number of
sample points give the estimate of
). A small number of
sample points give the estimate of  subject to considerable error. The
estimate of probability failure would approach the true value as
subject to considerable error. The
estimate of probability failure would approach the true value as 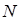 approaches infinity. Thus, the
accuracy of the estimation has been studied in several ways.
approaches infinity. Thus, the
accuracy of the estimation has been studied in several ways.
Variance of Estimation
One way would be to evaluate the variance or COV of
the estimated probability of failure. The COV can be estimated by
assuming each simulation to constitute a Bernoulli trial, and the number of
failure(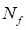 ) in
) in 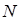 trials can be considered to follow a
binomial distribution. Then, the COV of the estimate
trials can be considered to follow a
binomial distribution. Then, the COV of the estimate  can be defined as
can be defined as
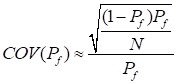
When you compare the results of Monte Carlo
Simulation, a smaller value of 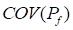 is more accurate result of them. The
above equation represents that COV approaches zero as
is more accurate result of them. The
above equation represents that COV approaches zero as 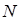 approaches infinity.
approaches infinity.
Confidence Interval of Estimation
Another way to study the error associated with the number of
simulations is by approximating the binomial distribution with a normal
distribution and estimating the 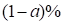 confidence interval of the estimated
probability of failure. It can be defined as
confidence interval of the estimated
probability of failure. It can be defined as
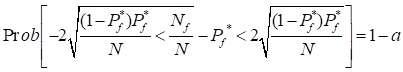
where  is
the exact probability of failure. The percentage error of the probability of
failure can be defined as
is
the exact probability of failure. The percentage error of the probability of
failure can be defined as
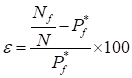
Combining those two equations, the percentage error can be
simplified as
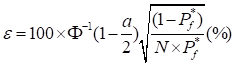
For example, for 10% error with 95% confidence,
the required number of samples is
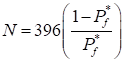
If  is 0.01, then the required
is 0.01, then the required 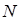 is 39,204 for 10% error with
95% confidence. Table 1 lists the required samples for 10% error with 95%
confidence interval.
is 39,204 for 10% error with
95% confidence. Table 1 lists the required samples for 10% error with 95%
confidence interval.
|
Prob |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
|
N |
39204 |
19404 |
12804 |
9504 |
7524 |
3564 |
1584 |
924 |
594 |
396 |
Table 1 The required
samples for exact probabilities (for 10% error with 95% confidence)
 may depend on the number of sample
points(
may depend on the number of sample
points(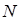 ). A small number of
sample points give the estimate of
). A small number of
sample points give the estimate of  subject to considerable error. The
estimate of probability failure would approach the true value as
subject to considerable error. The
estimate of probability failure would approach the true value as 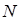 approaches infinity. Thus, the
accuracy of the estimation has been studied in several ways.
approaches infinity. Thus, the
accuracy of the estimation has been studied in several ways.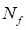 ) in
) in 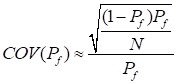
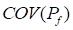 is more accurate result of them. The
above equation represents that COV approaches zero as
is more accurate result of them. The
above equation represents that COV approaches zero as 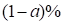 confidence interval of the estimated
probability of failure. It can be defined as
confidence interval of the estimated
probability of failure. It can be defined as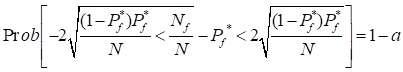
 is
the exact probability of failure. The percentage error of the probability of
failure can be defined as
is
the exact probability of failure. The percentage error of the probability of
failure can be defined as