
Two cantilever beam models shown in Figure 1 and 2 have a fixed-free end condition with ten lumped masses. One is modeled by using ten beam force elements and the other is modeled by using one flexible body of RecurDyn. The flexible beam model is originally generated in ANSYS. The material properties and geometric entity conditions of the beam are shown in Table 1.

Figure 1 Beam model using RecurDyn/Beam element

Figure 2 Beam model using RecurDyn/RFlex body element
|
Length |
0.4 m |
|
Mass |
3.9888 Kg |
|
Young’s modulus |
1x109 N/m2 |
|
Inertia of area |
1.215 x 10-8 m4 |
|
Area |
0.0018 m2 |
|
Damping ratio |
0.0 |
Table 1 The material properties and geometric entity conditions of beam
In Ref. 5, the analytic natural frequencies of these beams are computed as:
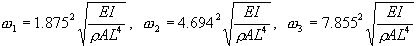 (1)
(1)
Substituting the values in Table4.2-1, the natural frequencies become

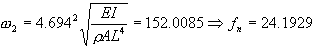
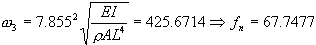
The eigenvalues of this beam model are validated against the analytic solution in Table 2.
|
Mode number |
Undamped Natural Frequency (Hz) | ||
|
Beam element |
Flexible Body |
Analytic solution | |
|
1 |
3.84002E+00 |
3.84259E+00 |
3.8426 |
|
2 |
2.37455E+01 |
2.38154E+01 |
23.8154 |
|
3 |
6.55744E+01 |
6.60152E+01 |
66.0152 |
|
4 |
1.26483E+02 |
1.28016E+02 |
128.016 |
Table 2 Eigenvalues of the cantilever beam model
In addition, RecurDyn can show the mode shapes of the beam model through 3D animation, as shown in Figures 3 and 4.
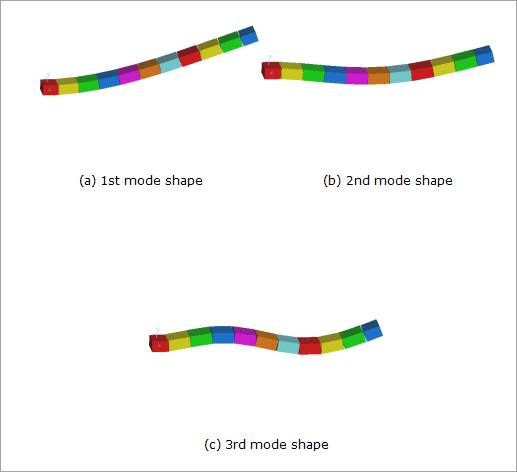
Figure 3 Mode shapes of the beam model through 3D animation
The mode shapes of the model using RecurDyn/Beam element
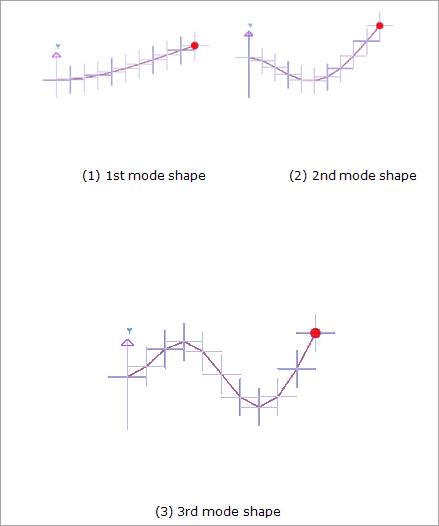
Figure 4 Mode shapes of the beam model
The mode shapes of the model are using RecurDyn/RFlex.